Vollständige Induktion am Beispiel der Summe der natürlichen Zahlen.

Rémy Schumm, für KI 1b

8. Februar 2000

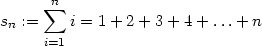
Zusammenfassung des ersten Beispiels von Pfenniger.

1 Definitionen

Sei

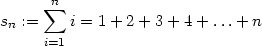sum n sn := i = 1+ 2+ 3 + 4+ ...+ n i=1
(1)

die Summe der natürlichen Zahlen von 1 bis n. sn ist gegeben durch die Rekursion:

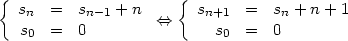{ sn = sn-1 + n { sn+1 = sn + n + 1 s = 0 <==> s = 0 0 0
(2)

2 Behauptung / Satz

Satz: Es gilt die explizite Formel für sn:

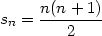n(n+ 1) sn = ---2----
(3)

Die Aufgabe ist es nun, diese Formel 3 zu beweisen.

3 Beweis durch vollständige Induktion

3.1 Plan und Überlegungen:

3.1.1 Verankerung
Als erstes wird bewiesen, dass die sn für irgend ein n gilt, z.B. für n = 0 oder so. Dann sind wir sicher, dass es irgendwo mal stimmt.
3.1.2 Induktionsschritt
Als zweites nehmen wir an (=Induktionsannahme), wir hätten die Formel 3 für irgendein n schon bewiesen, z.B. für n = 57. Wenn wir nun beweisen können, dass die Formel 3, die aufgrund der (Induktions-)annahme für n schon gilt, auch für n + 1 gilt, haben wir die ganze Geschichte bewiesen.
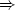Nämlich: Für n = 0 ist die Sache ja eh ok. Mit dem Induktionsschritt beweisen wir aber, dass 3 für n = n + 1 = 0 + 1 = 1 auch gilt. Aber dann gilt sie auch für n = 3 etc. etc. ==> die Formel 3 gilt 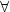A n (- N.

3.2 Durchführung

Beweis der Formel 3:

3.2.1 Verankerung
Sei n = 0, wir überprüfen die Formel 3:
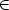
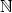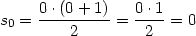0.(0 + 1) 0.1 s0 = ----2----= -2--= 0
(4)

...und das steht ja schon in der Definition 2, also ist die Verankerung gegessen.

3.2.2 Induktionsschritt

Induktionsannahme: Wir nehmen an, Formel 3 gelte für irgendein n, also z.B., weil wir ja schliesslich bei Herrn Pfenniger Schule haben, bei n = 57:

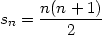n(n+ 1) sn = ---2----
(5)

Iduktionsbehauptung: Wir wollen nun zeigen, dass 3 auch für n + 1 gilt, also:

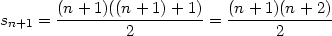(n-+-1)((n-+-1)-+-1) (n+-1)(n-+-2) sn+1 = 2 = 2
(6)

Beweis der Induktionsbehauptung: Nach der Definition unserer sn (Formel 2) gilt ja:

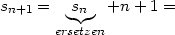sn+1 = sn +n + 1 = ersetzen
(7)

Ich ersetze sn durch den Ausdruck in der Induktionsannahme 5:

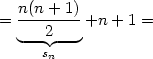n(n + 1) = --------+n + 1 = --2 --- sn
(8)

Mit ein Bisschen Umformen ist das aber:

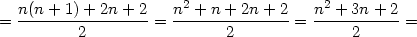2 2 = n(n+-1)-+-2n-+-2-= n--+-n+-2n-+-2-= n-+-3n-+-2-= 2 2 2
(9)

Durch Faktorisierung (bzw. Schielen auf Gleichung 6) sieht man, dass das gleich folgendem ist:

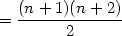(n + 1)(n + 2) = ------2------
(10)

Das ist nun aber, was wir in der Behauptung 6 beweisen wollten. Damit ist nun also unsere Induktionsbehauptung bewiesen, damit der Induktionsschritt, und damit die ganze Induktion.
Wir haben bewiesen, dass die explizite Formel 3 für alle natürlichen Zahlen n 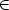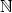(- N gilt.

Typeset in LATEX2eusing OzTEX2.1 on PowerMacintosh G3.
Quellcode: vollInd.tex