Crashkurs für Gaussalgorithmus

Rémy Schumm, für KI 1b

17. Februar 2000

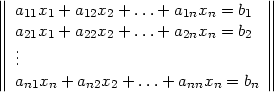
Ein Verfahren, um lineare Gleichungssysteme aufzulösen.

1 Definitionen

lineares Gleichungssystem Ein lineares Gleichungsystem mit n Gleichungen und n Unbekannten x sieht so aus:

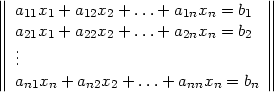|| || |||| a11x1 + a12x2 + ...+ a1nxn = b1 |||| |||| a21x1 + a22x2 + ...+ a2nxn = b2 |||| |||| .. |||| || . || || an1xn + an2x2 + ...+ annxn = bn ||
(1)

Das Gleichungssystem kann auch in Matrixform dargestellt werden:

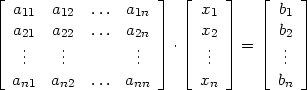|_ a11 a12 ... a1n _| |_ x1 _| |_ b1 _| a a ... a x b 2.1 22. 2.n . 2. = .2 |_ .. .. .. _| |_ .. _| |_ .. _| an1 an2 ... ann xn bn
(2)

oder kurz

Ax = b
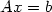(3)

Das ist eigentlich “nur” eine andere Schreibweise.

2 Ziel

Man löst nun das Gleichunsystem, indem man es in die Form

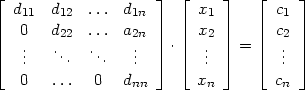|_ _| |_ _| |_ _| d11 d12 ... d1n x1 c1 0 d22 ... a2n . x2 = c2 |_ ... ... ... ... _| |_ ... _| |_ ... _| 0 ... 0 d x c nn n n
(4)

bringt, und nachher rückwärts aufllöst:
Aus der letzten Zeile kann man xn ausrechnen. Han man aber xn, kann man mit der zweitletzten Zeile xn-1 ausrechnen; etc...
Die Gleichungssysteme 4 und 2 haben die gleiche Lösung x1...xn. (Nein, das beweise ich nicht.)

3 Vorgehen

Das Vorgehen ist eigentlich das gleiche, wie wenn man ein Gleichungsystem von Hand löst:
Man nimmt Zeilen von A und b, multipliziert sie mit geeigneten Faktoren und zählt sie voneinander ab bzw. addiert sie:
Weil das mit Indexen und so recht kompliziert ist 1 und ich es auch nicht mehr so genau weiss (und mein LATEX2eCompiler sowieso heute dauernd auf die Nase fällt 2, was aber an mir liegt), mache ich einfach ein

Beispiel: Gegeben sei das 3 . 3 Gleichungssystem

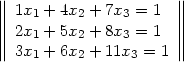|||| |||| || 1x1 + 4x2 + 7x3 = 1 || |||| 2x1 + 5x2 + 8x3 = 1 |||| || 3x1 + 6x2 + 11x3 = 1 ||
(5)

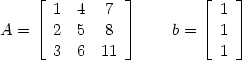
was also folgendem A und b entspricht:

|_ _| |_ _| 1 4 7 1 A = |_ 2 5 8 _| b = |_ 1 _| 3 6 11 1
(6)

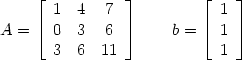
Ich nehme nun Zeile 1 mit 2 multipliziert und ziehe die zweite davon ab: Das Ergebnis schreibe ich in die 2. Zeile:

|_ 1 4 7 _| |_ 1 _| |_ _| |_ _| A = 0 3 6 b = 1 3 6 11 1
(7)

Das gleiche mit Zeile 1 mit 3 multiplieziert und die dritte abziehen:

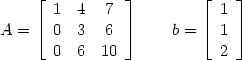|_ 1 4 7 _| |_ 1 _| A = |_ 0 3 6 _| b = |_ 1 _| 0 6 10 2
(8)

Nun das gleiche mit den beiden letzten Zeilen: Zeile 2 mit 2 multiplieren, Zeile 3 davon abziehen:

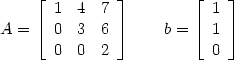|_ _| |_ _| 1 4 7 1 A = |_ 0 3 6 _| b = |_ 1 _| 0 0 2 0
(9)

Wir haben unser System 5 also in die folgende Form gebracht:

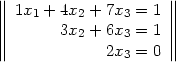|| || |||| 1x1 + 4x2 + 7x3 = 1 |||| |||| 3x2 + 6x3 = 1 |||| || 2x3 = 0 ||
(10)

Das kann man nun einfach lösen, indem man rückwärts einsetzt: man erhält:

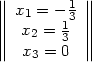|||| x1 = - 1 |||| |||| x = 13 |||| |||| 2 3 |||| x3 = 0
(11)

Und nun gehe ich schlafen.

Typeset in LATEX2eusing OzTEX4.0 on iBook.
Quellcode: gauss.tex
nach: Prof. Jürg Marti, Numerische Mathematik I (2.1, Ordner V), ETH Zürich, 199?