Integrale

Die wichtigsten Regeln.

1 Grundeigenschaften, Linearität.

Vertauschen der Integrationsgrenzen:

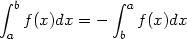integral b integral a a f (x)dx = - b f(x)dx
(1)

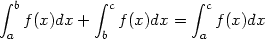integral b integral c integral c f(x)dx+ f(x)dx = f(x)dx a b a
(2)

Linearität:

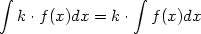integral integral k .f(x)dx = k . f(x)dx
(3)

integral integral integral [k .f(x)+ l .g(x)]dx = k . f(x)dx + l . g(x)dx
(4)

2 Integrations-Rechenregeln.

Sie F(x) eine Stammfunktion von f(x), G(x) von g(x): Es gelte also F'(x) = f(x) bzw. 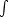integral f(x)dx = F(x) + const etc.

Partielle Integration:

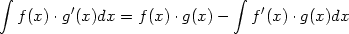integral integral ' ' f(x).g (x)dx = f(x).g(x) - f (x).g(x)dx
(5)

Integration durch Substitution:

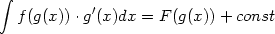integral f (g(x)).g'(x)dx = F (g(x)) + const
(6)

Bem.: Die Gleichungen 5 ist das Pendant zur Produktregel in der Ableitungstheorie, bzw. Gleichung 6 zur Kettenregel (”innere Ableitung”).

3 Hauptsatz der Infinitesimalrechung.

Der Hauptsatz der Infinitesimalrechnung sagt etwa: Das Integral ist die Umkehrung der Ableitung. Also: leitet man eine Funktion ab, und integriert sie dann, bekommt man wieder das gleiche. Und umgekehrt auch. Formal (mit Integrationsgrenzen) sieht das so aus:

integral x d-- ' const+ F (x) = a f(t)dt ==> dxF (x) =_ F (x) = f (x)
(7)

Und umgekehrt:

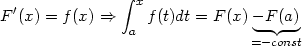integral x F '(x) = f(x) ==> f(t)dt = F(x) -F-(a) a =-const
(8)

4 Einige wichtige Stammfunktionen:

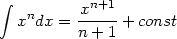integral xn+1 xndx = -----+ const n + 1
(9)

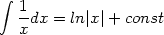integral -1 x dx = ln| x |+ const
(10)

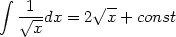integral -1- V~ -- V~ x-dx = 2 x+ const
(11)

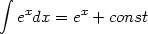integral x x e dx = e + const
(12)

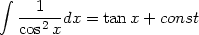integral --1--- cos2x dx = tanx + const
(13)

Im Übrigen soll man immer auf die Listen der Ableitungsrechung zurückgreifen:
Bsp.: Es soll 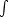integral cosxdx berechnet werden: Man weiss:

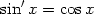sin'x = cosx
(14)

aus der Differentialrechung. Will man also das Integral von cosx berechnen, lese man 14 rückwärts und erhaltet:

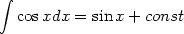integral cosxdx = sinx + const
(15)

Das funktionniert mit allen bekannten Ableitungen. Weiss man also, dass eine zu integrierende Funktion die Ableitung von etwas ist, ist dieses Etwas die Lösung des Integrals.
als LATEX- Übung, ©rs März 1997, rschumm@g26.ethz.ch