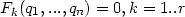
Ich beginne meinen Vortrag, indem ich ich erst von Zwangsbedingungen in Bewegungen rede und dann dazu übergehe zu zeigen, wie es mit der Lagrange Mechanik gelingt, diese zum Teil recht mühsamen Zwangsbedingungen zu eliminieren.

1 Zwangsbedingungen

Ich beschreibe den Konfigurationsraum meines mechanischen Systems, indem ich allgemeine Koordinaten q_i einführe, die dem Konfigurationsraum angepasst sind. Es gelten im Folgenden Zwangsbedingungen, die durch folgendes beschrieben werden:

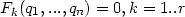(1)

Im weiteren nehme ich an, diese Gleichungen seien voneinander unabhängig, d.h. nach dem Satz über implicite Funktionen gilt:

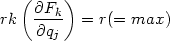(2)

Solche Zwangsbedingungen nennt man holonom. Die Anzahl Freiheitsgrade ist f = n - r.

Trajectorie Ich definiere jetzt einen Weg in diesem Raum, genannt Trajectorie:

(3)

Die Virtuelle Verrückung wird definiert als:

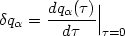(4)

Wegen 1 ist (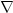F_k,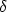q) = 0, d.h.

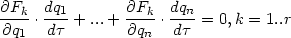(5)

Satz von Froebenius Vorhin habe ich von holonomen Zwangsbedingungen gesprochen, solche, die die Bewegugnsfreiheit von unserem System global einschränken. Nun, was sind aber nicht holonome Zwangsbedingungen? Das sind dann solche, die die Bewegungen nur local, infinitesimal einschränken; am besten man stellt sich ein Rad auf einer Ebene vor: das kann sich infinitesimal nur in einer Richtung bewegen (in die es gerade rollt), aber global kann es natürlich in jeden beliebigen Punkt der Ebene gelangen. Der Satz von Froebenius liefert uns ein mathematisches Kriterium zur Unterscheidung von holonomen und nicht-holonomen Zwangsbedingungen.
Ich will nun anstelle der 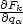in der Gleichung 5 bei den holonomen Zwangskräften die Zwangskräfte nun mit _k beschreiben. Wann sind nun also die Gleichungen

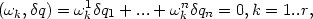(6)

welche nun die Zwangsbedingungen beschreiben, mit den obigen Gleichungen 1 äquivalent? Das Kriterium liefert der Satz von Froebenius:
Die Zwangsbedingungen sind holonom, genau dann wann 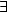Funktionen J₁,...,J_r sodass

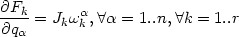(7)

oder local gilt 7 genau dann wann

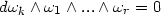(8)

In Worten: die Zwangsbedingungen sind von der Form 1 genau dann wenn die obigen Gleichungen erfüllt sind. Solche, die die obigen Sachen nicht erfüllen, sind also nicht holonom.

2 Zwangskräfte

Zwangskräfte sind Kräfte, die durch die Zwangsbedingungen erzeugt werden; sie stehen immer senkrecht zu den virtuellen Verrückungen 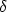q. Zwangskräfte leisten keine virtuelle Arbeit, sie stehen senkrecht zu den virtuelle Verrückungen; es gilt also:

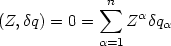(9)

Im folgenden betrachte ich wieder Zwangsbedingungen der Form

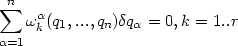(10)

Vergleich von 10 und 9 führt zum Schluss, dass gelten muss:

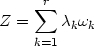(11)

Das werden wir später wieder gebrauchen.

Mechanisches Gleichgewicht Sei nun F eine äussere, treibende Kraft. Die Bedingung für ein mechanisches Gleichgewicht ist, dass die treibenden Kräfte die Zwangskräfte aufheben müssen: Es gilt:

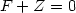(12)

Man kann also sagen, die Projektion der treibenden Kräfte auf den Tangentialraum der Zwangskräfte ist Null.

3 Dynamik und Lagrange-Gleichung 1^er Art.

Nun will ich zu den bewegten Dingen übergehen:
Ich betrachte ganz klassisch N Massenpunkte und stelle die Newton’schen Gleichungen für ein solches System mit Zwansgbedingungen:

(13)

wobei die 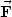_i die treibenden Kräfte sind und die 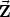_i die Zwangskräfte.
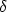
Es ist eine unumstrittene Tatsache, dass die virtuellen Verrückungen 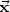_i,i = 1..N senkrecht zu den 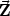_i sind. Es muss also für alle N Massenpunkte gelten (wie in 9 schon gesehen), dass

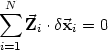(14)

Analog wie in 10 sind jetzt wieder die virtuellen Verrückungen eingeschränkt durch folgende Zwangsbedingungen, welche nicht unbedingt holonom sein müssen:

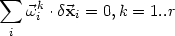(15)

Wiederum folgt aus den Gleichungen 14 und 15, dass für die 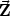_i gelten muss:

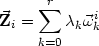(16)

Setzt man dies in 13 ein, erhält man die Langrange Gleichungen 1^er Art:

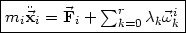(17)

Diese Gleichungen können sehr behilflich sein, wenn man ein System lösen will, dass z.T. eben nicht-holonome Zwangsbedingungen enthält.

4 Lagrange-Gleichungen 2^er Art.

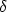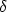
d‘Alembert‘sches Prinzip Ich möchte als ersten Schritt zur Herleitung der Lagrange-Gleichungen 2^er Art das d‘Alembert‘sche Prinzip zeigen: man führe eine virtuelle Arbeit A^* ein, die man durch Multiplikation der Gleichung 13 mit 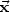_i erhält:

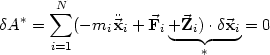(18)

Der Teil * ist wegen 14 Null, man erhält also folgende Bewegungsgleichung, wo die Zwangskräfte 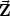_i nicht mehr vorkommen:

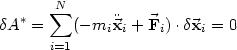(19)

Diese Gleichung nennt man das d‘Alembert‘sche Prinzip.

System mit nur holonomen Zwangsbedingungen Nun weiter: man betrachte nun ein System von N Massenpunkten im Raum ³ mit f Freiheitsgraden. Die Teilchen seien durch 3N - f ausschliesslich holonome Zwangsbediungungen eingeschränkt. Vorher hatte ich für die Koordinaten der Massenpunkte 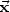_i benützt, jetzt kann ich also f allgemeine Koordinaten q einführen, i = 1..N:

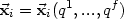(20)

Die zulässigen virtuellen Verrückungen sind dann:

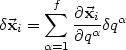(21)

Das d‘Alembert‘schen Prinzip (19) führt dann direkt auf folgende Bewegungsgleichungen (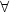 = 1..f)

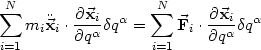(22)

Mit der kinetischen Energie

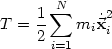(23)

kommt man dazu, dass die obigen Gleichungen 22 zu den folgenden äquivalent sind ():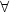

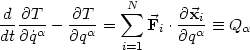(24)

Q ist eine verallgemeinterte Kraft. Man nehme nun ein V sodass gelte

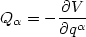(25)

mit 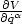= 0. Das geht, falls die 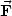_i Potentialkräfte sind, also gilt

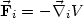(26)

dann gilt nämlich 24:

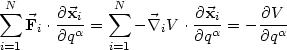(27)

und setze das V schliesslich in 24 ein:

(28)

und formt um

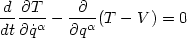(29)

was dann ergibt

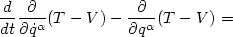(30)

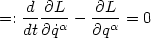(31)

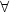
, mit L := T - V die Lagrange Funktion. Diese Gleichungen sind also äquivalent zu unseren obigen Bewegunsgleichungn 22 und heissen Lagrangegleichungen 2^er Art oder Euler-Lagrange-Gleichungen.

5 Euler-Lagrange Gleichungen im Variationsprinzip

Gelegentlich trifft man die Euler-Lagrange Gleichungen in einem anderen Zusammenhang an, in dem der Variationsrechunung. Dort definiert man ein Funktional S auf den Raum aller Trajectorien in ³, genannt die Wirkung:

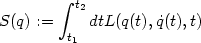(32)

Es gibt dann eine spezielles q_*, sodass S(q_*) ein Extremum hat, beziehungsweise 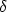S(q_*) = 0, genau dann wenn es die Euler-Lagrange-Gleichungen

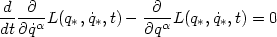(33)

erfüllt. Das nennt man das Hamilton-Prinzip, das also äquivalent ist zum obigen d‘Alembert-Prinzip 19.